Rumus simpangan rata-rata adalah salah satu rumus yang sering digunakan dalam bidang matematika. Rumus sendiri berfungsi untuk menghitung sesuatu supaya mendapatkan informasi mengenai jumlah data secara keseluruhan.
Sedangkan simpangan rata-rata adalah nilai rata-rata dari selisih setiap data dengan nilai mean atau rataan hitungnya. Deviasi rata-rata sering dilambangkan dengan SR.
Rumus simpangan rata-rata biasanya digunakan untuk menentukan ukuran dan penyebaran data dalam salah satu analisis data deskriftif.
Keragaman atau variasi setiap kumpulan data bisa diukur dengan memakai suatu nilai numeric yang disebut sebagai ukuran penyebaran data atau ukuran keragaman data. Salah satu ukuran penyebaran data adalah simpangan rata-rata.
Rumus Simpangan Rata-rata
Perlu diketahui bahwa secara umum, rumus simpangan rata-rata dibagi menjadi dua, yakni simpangan rata-rata data tunggal dan simpangan rata-rata berkelompok.
Untuk lebih jelasnya yuk kita simak penjelasan mengenai rumus simpangan rata-rata beserta contoh soalnya sebabagai berikut ini.
1. Rumus Simpangan rata-rata tunggal

Keterangan:
SR: simpangan rata-rata
X: data ke-i, ada juga yang menyimbolkan dengan xi
X dengan akses graris di atas: nilai rata-rata data
n: banyak data
Contoh soal 1:
Nilai ulangan Bahas Inggris dari 6 siswa adalah: 7, 5, 6, 3, 8, 7. Berapa simpangan rata-ratanya?
Jawaban: {-1+1+0+3+(-2)+(-1)}/6: 0
SR = 6
Contoh soal 2:
Simpangan rata-rata dari data 2, 4, 5, 8, 3, 8 adalah?
Diketahui:
n = 6
Lalu anda perlu mencari x dengan aksen garis di atasnya (nilai rata-rata). Caranya adalah dengan membagi jumlah seluruh data dengan banyaknya data.
Jadi:
x aksen = 2+ 4+5+ 8+3+8 : 6
x aksen = 30 : 6 = 5
Maka, x aksen = 5
Selanjutnya anda bisa mencari simpangan rata-rata sebagai berikut:
SR = (∑|2-5|+ |4-5|+ |5-5|+ |8-5|+ |3-5|+ |8-5|)/6
SR = (∑|-3|+ |-1|+ |0|+ |3|+ |-2|+ |3|)/6
SR = 0/6
SR = 0
Jadi simpangan rata-rata data tunggal di atas adalah 0
2. Rumus Simpangan rata-rata kelompok
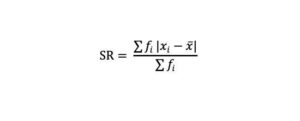
Keterangan:
SR: simpanan rata-rata
Xi: data ke-i
x aksen: nilai rata-data data
fi atau f: total frekuensi
Contoh soal:
Coba anda cari simpangan rata-rata dari data dibawah ini:
| Interval Nilai | Frekuensi |
| 1-3 | 8 |
| 4-6 | 4 |
| 7-9 | 3 |
| 10-12 | 3 |
| 13-15 | 2 |
Untuk dapat mencari simpangan rata-rata data di atas, anda perlu mencari tahu dulu nilai tengah (xi). Sebab, nanti di akhir anda membutuhkan nilai x aksen yang didapat dari xi dikali fi. Maka, tabelnya menjadi:
| Intervensi Nilai | Frekuensi (fi) | Nilai tengah (xi) | Fi.xi |
| 1-3 | 8 | 2 | 16 |
| 4-6 | 4 | 5 | 20 |
| 7-9 | 3 | 8 | 24 |
| 10-12 | 3 | 11 | 33 |
| 13-15 | 2 | 14 | 28 |
| Total | 20 | 105 |
Selanjutnya adalah mencari x aksen dengan menggunakan rumus dibawah ini:
x aksen = (fi.xi)/fi
x aksen = 105/20
x aksen = 5,25
Langkah selanjutnya adalah anda perlu mencari simpangan rata-rata dari masing-masing interval data untuk menentukan ∑ fi,xi aksen pada rumus. Caranya adalah:
| Interval nilai | (fi) | (xi) | Fi.xi | |xi-x aksen| | Fi|xi-x aksen| |
| 1-3 | 8 | 2 | 16 | |2-5,25| = -3,25 | -26 |
| 4-6 | 4 | 5 | 20 | |5-5,25| = -0,25 | -1 |
| 7-9 | 3 | 8 | 24 | |8-5,25| = 2,75 | 8,25 |
| 10-12 | 3 | 11 | 33 | |11-5,25| = 5,75 | 17,25 |
| 13-15 | 2 | 14 | 28 | |14-5,25| = 8,75 | 17,25 |
| Total | 20 | 105 | 12,75 |
Langkah yang terakhir, anda masukkan hasilnya ke rumus awal untuk mencari simpangan rata-rata.
SR = 12,75 : 20 = 0,6375